【前沿】持续学习赋能 Koopman 动力学:足式机器人线性控制范式新突破
Continual Learning and Lifting of Koopman Dynamics for Linear Control of Legged Robots(基于持续学习与提升的Koopman动力学在足式机器人线性控制中的应用)是一个结合了现代控制理论、机器学习以及机器人动力学的前沿研究方向。

1 / Koopman
一、Koopman理论的核心创新与机器人控制范式转变
Koopman算子理论:
Koopman算子通过将非线性动力学系统映射到高维线性特征空间,使得原本复杂的非线性系统在该空间中表现为线性演化。这一理论为足式机器人(如四足、双足机器人)的控制提供了新的思路,因为这类机器人通常具有高度非线性的动力学特性。
持续学习(Continual Learning):
在机器人控制中,持续学习指系统能够在不断变化的环境中(如不同地形、负载条件)持续优化控制策略,而不会遗忘先前学到的知识。这对于足式机器人尤为重要,因为它们需要在复杂、动态的环境中保持稳定性和适应性。
线性控制:
通过Koopman提升,将非线性动力学转化为线性模型后,可以利用成熟的线性控制理论(如LQR、MPC)设计控制器,从而简化控制算法的设计和实现。
2 / Koopman
二、持续学习框架的关键技术路径
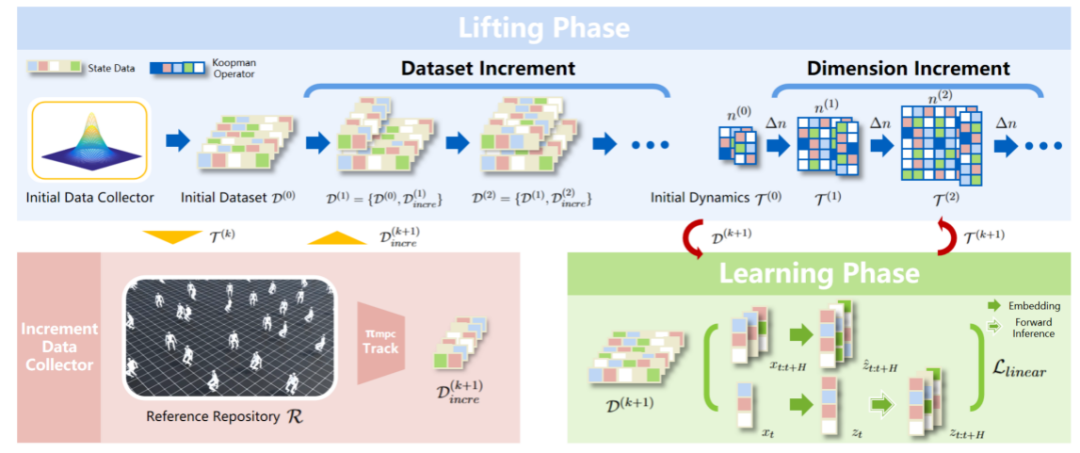
数据驱动的Koopman算子学习:
利用机器人运动数据(如关节角度、速度、力矩等),通过数据驱动的方法(如动态模式分解DMD、深度学习)学习Koopman算子及其特征函数。这些特征函数将原始状态空间映射到高维线性空间。
持续学习框架:
结合持续学习算法(如弹性权重巩固EWC、渐进神经网络ANN),在不断接收新数据的同时,防止对先前任务(如不同地形行走)的遗忘。
线性控制器设计:
在提升后的线性空间中,设计线性控制器(如状态反馈控制器、模型预测控制器MPC),并通过逆映射将控制指令转换回原始状态空间,实现对机器人的实际控制。
3 / Koopman
三、足式机器人控制应用与验证
复杂环境适应性:
足式机器人需要在不同地形(如平地、斜坡、楼梯)上运行,Koopman提升后的线性模型能够更高效地处理这些复杂环境下的动力学变化。
控制算法简化:
线性控制理论成熟且计算效率高,相比直接处理非线性动力学,能够显著降低控制算法的复杂度和计算成本。
持续学习能力:
通过持续学习,机器人能够不断积累经验,适应新的任务和环境,而无需重新训练整个模型。

4 / Koopman
四、技术挑战与未来方向
高维Koopman空间的学习:
Koopman提升后的空间维度通常较高,可能导致计算复杂度增加和过拟合问题。需要开发高效的降维方法(如稀疏Koopman模式选择)。
持续学习中的稳定性:
在不断学习新任务的同时,如何保持对旧任务的稳定控制是一个关键挑战。需要设计有效的正则化方法或记忆回放机制。
实时性要求:
足式机器人控制需要实时响应,而Koopman算子的学习和线性控制器的设计需要满足实时性要求,这对算法的效率提出了高要求。
5 / Koopman
五、研究进展
模型学习:
近期研究提出了基于深度学习的Koopman算子学习方法(如VAMPnets),能够自动学习系统的Koopman特征函数,减少了人工设计特征函数的复杂性。
持续学习与Koopman结合:
一些研究开始探索如何将持续学习与Koopman动力学相结合,例如通过元学习(Meta-Learning)方法快速适应新环境。
实验验证:
在仿真和实际机器人平台上(如ANYmal、MIT Cheetah),研究者验证了Koopman提升后的线性控制器在足式机器人运动控制中的有效性。

6 / Koopman
六、未来方向
多任务学习:
探索如何在一个统一的Koopman框架下处理多个任务(如行走、奔跑、跳跃),进一步提升机器人的通用性。
物理可解释性:
尽管Koopman理论提供了强大的建模能力,但其高维特征空间的物理意义尚不明确。未来研究可以关注如何增强模型的物理可解释性。
硬件实现:
将Koopman控制方法部署到实际机器人硬件上,验证其在真实环境中的性能和鲁棒性。
Continual Learning and Lifting of Koopman Dynamics for Linear Control of Legged Robots 是一个具有广阔前景的研究方向,它结合了Koopman动力学的非线性系统线性化能力与持续学习的适应性,为足式机器人的高效控制提供了新的解决方案。尽管面临高维学习、持续稳定性等挑战,但随着深度学习和控制理论的进一步发展,这一领域有望在机器人自主运动、复杂环境适应等方面取得突破性进展。